01-solution

0001/01/01

Note that due dates can be found in the Syllabus; submission instructions can be found on the Assignment Instructions page. In this assignment, you can submit a Google Doc (or other text editor, pictures, etc.) but also your \({\tt R}\) code via Google Drive. Samira will go over the submission process in the lab.

\({\bf 60}\) total marks.

Question 1 [7 points] You obtained a \({\tt gmail}\) account for this course. With this account, you can also initiate your Google Drive workspace. (i) Does Google have the right to look at your emails, documents, drawings or other objects? (ii) Does Google have the right to use this information? What is meta-data? Can it collect meta-data about your information? (iii) How can you turn on or off the geographical tracking mechanism associated with your account? (iv) Are you satisfied with the level of security and user agreement with Google? (Answer in ~10 sentences please.)

  1. Google has the right to look at and collect any content that you provide to them
  2. Google has the right to use the information you give to them although it promises that it doesn’t sell your data and just use it to make the ads relevant to your need. Meta-data is the “data about data”. The data that describes and gives information about other data. Google can and does collect the meta-data about your information.
  3. You can do it by going to the “Location History” section of your Google account and turn it off or on. iv)answer as your personal opinion.

Question 2 [10 points] Given what you read about Google, highlight any differences with Apple Cloud or other Cloud service provider of your choice. Comment overall on what you found.

Answer Apple Cloud offers better security compare to Google as Google offers no end-to-end encryption. It means that the data can be accessed by anyone that Google provide the data to. However, Google Drive is accessible from all platform while Apple Cloud is just accessible from Apple devices. Google provides more free storage than Apple. Google also is better for collaboration as its features are more useful for that matter. In general, Google is a better provider compare to many other platforms.

Question 3 [3 points] Explain how cloud computing can reduce the overall cost for computers and computation for a small business or research group? If so, how? Make reference to the definitions and components of cloud and traditional computing from the lecture notes. 4 or 5 sentences.

Answer Cloud computing can reduce the overall cost and save time for small business by providing stores data, improving their productivity and collaboration and also promoting innovation. With cloud computing, small businesses can have access information wherever and whenever they want. The data always synced between all people in the group therefore members have access to the most recent version of their documents. As there is no need for business owner to buy and maintain server equipment anymore, the labor cost to maintain the server would not be an issue anymore. Although they still should pay for cloud services monthly, it is more manageable and cheaper than before.

Question 4 [4 points] Argue for and against each of the following items as a computing device (make references to the 3 fundamental properties of modern computers).

  1. a bacterium
  2. a plant
  3. a squid
  4. a human
  5. an assembly line to make household appliances

Answer Your answer (for or against) should mention all the properties: Property 1: Input → algorithm → output Property 2: Notion of reprogrammability Property 3: Notion of state and memory

Question 5 [4 points] Create an \({\tt R}\) script under \({\tt File/NewFile}\). Write R code to load the \({\tt tidyverse}\) library and the \({\tt small\_brca}\) dataset. Note that in the course slides, I load the dataset from my directory specific to my computer. However, if you look in the R code in the \({\tt src}\) on RStudio Cloud (Project 03), you will find the correct path for you.

Make a comment that this is Question 5, Assignment 1 before your code. Find the function in \({\tt R}\) that reports the date and the version of \({\tt R}\) that you are using. Put the code in your file.

Save your R code in your \({\tt src}\) directory of the project and name the file \({\tt lastname\_assignment1.R}\). Take a screenshot with your file open (top left), the Environment list showing (top right), the code executed in your R session (bottom left), and the contents of the \({\tt src}\) folder (bottom right). Congratulations, you are now an R programmer.

##                _                           
## platform       x86_64-apple-darwin17.0     
## arch           x86_64                      
## os             darwin17.0                  
## system         x86_64, darwin17.0          
## status                                     
## major          4                           
## minor          0.3                         
## year           2020                        
## month          10                          
## day            10                          
## svn rev        79318                       
## language       R                           
## version.string R version 4.0.3 (2020-10-10)
## nickname       Bunny-Wunnies Freak Out
## [1] "Mon Nov 15 11:41:19 2021"

For Questions 6-8 below. Put a comment in your file that states what question you are working on and put your code below it. For any pictures (eg the plot that your code generates) and text, put them into a text document (eg using Google Docs) stating what question you are working on.

Question 6 [5 points]

Recall from the lecture that \({\tt HER2}\) is an important protein in some subtypes of breast cancer, and remmeber that \({\tt ERBB2}\) is the official name for \({\tt HER2}\).

The variable \({\tt ERBB2}\) in our tibble corresponds to estimates of the number of transcripts present in each sample (row). This is obtained using RNA-seq technologies as discussed in the lecture. Clinically, \({\tt HER2}\) is not measured using transcriptomics. Typically the copy number of \({\tt HER2}\) is measured at at the DNA level. This is because we believe that \({\tt HER2}\) over-expression at the transcript and protein levels are due to a amplification of the genomic region tha contains \({\tt HER2}\). In the clinic, Fluorescence In Situ Hybridization (FISH) is used.

The variable \({\tt her2\_fish\_status}\) gives exactly this, although it is not available for many observations (rows/patient samples).

Using ggplot, making the following scatter plot. Put your R code with your answer.

ggplot(data = small_brca) + 
  geom_point(mapping = aes(x = ERBB2,  y = GRB7, color = her2_fish_status, shape=tumor), size = 2)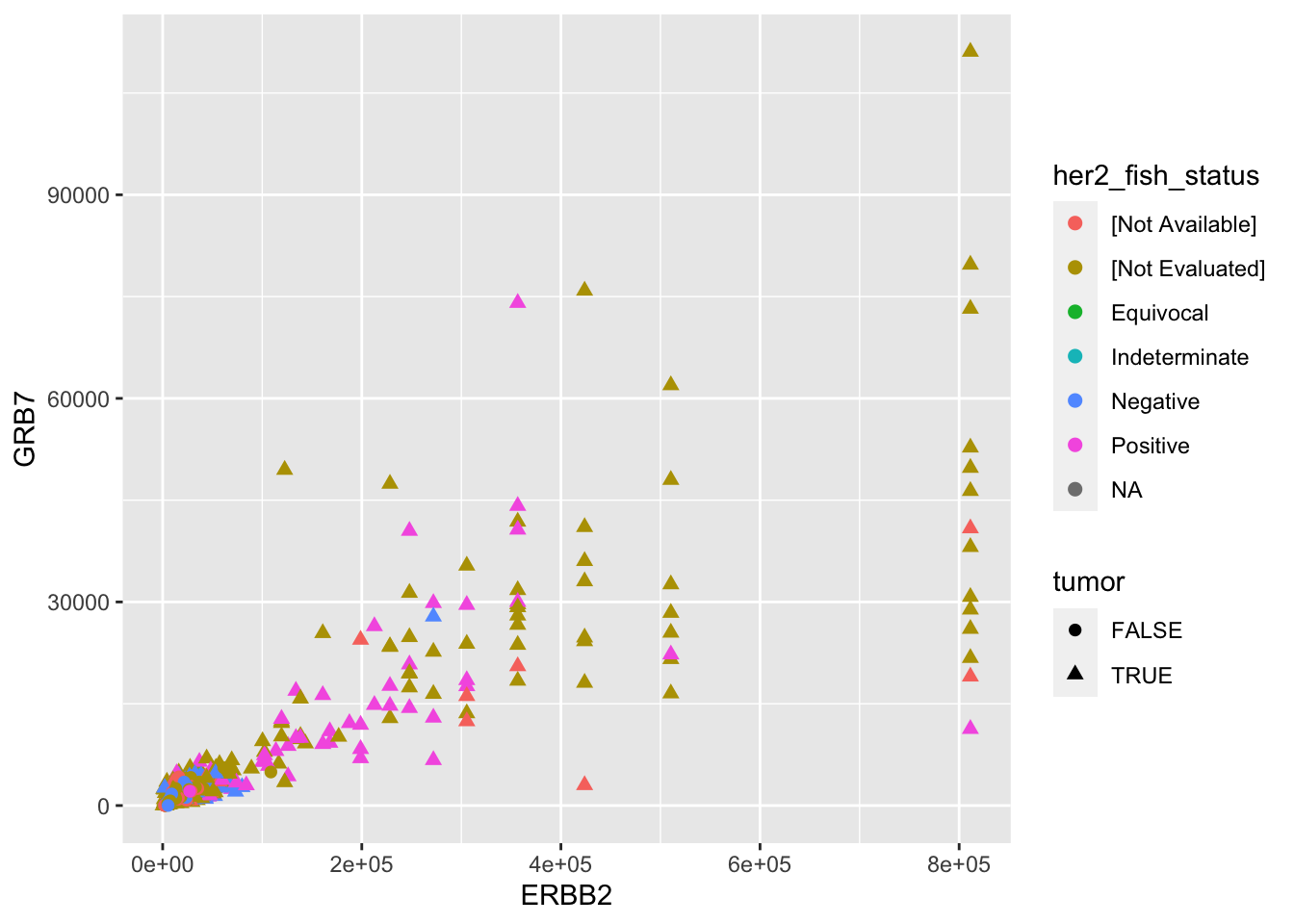

Comment or interpret the graph in 1 or 2 sentences: does it make sense? is it what you expected? are there issues? etc.

Question 7 [5 points]

It is a little bit hard to see the status of \({\tt tumor}\) and \({\tt her2\_fish\_status}\) in the figure of Question 6 because so many points are bunched up around the origin of the graph. Using online resources, figure out how to log-transform the both the \(x\) and \(y\) axis. Log-transformations will be revisited several times but they are very common transformations of gene expresion data. Recreate the scatterplot with the log-transformed data. Show your code and the image it generates. Comment on whether this transformation helped and if it changes your conclusions from Question 6.

ggplot(data = small_brca) + 
  geom_point(mapping = aes(x = GRB7,  y = ERBB2, color = her2_fish_status, shape=tumor), size = 2) +
   scale_x_log10()+
  scale_y_log10()

Question 8 [7 points]

Create a boxplot in \({\tt ggplot}\) as below. Hint: I logged transformed the expresion of \({\tt ERBB2}\)). Comparing positive and negative samples, is there any hypotheses you could form?

Answer

ggplot(data = small_brca,  aes(x=factor(her2_fish_status), y=log(ERBB2), fill=tumor))  + 
  geom_boxplot()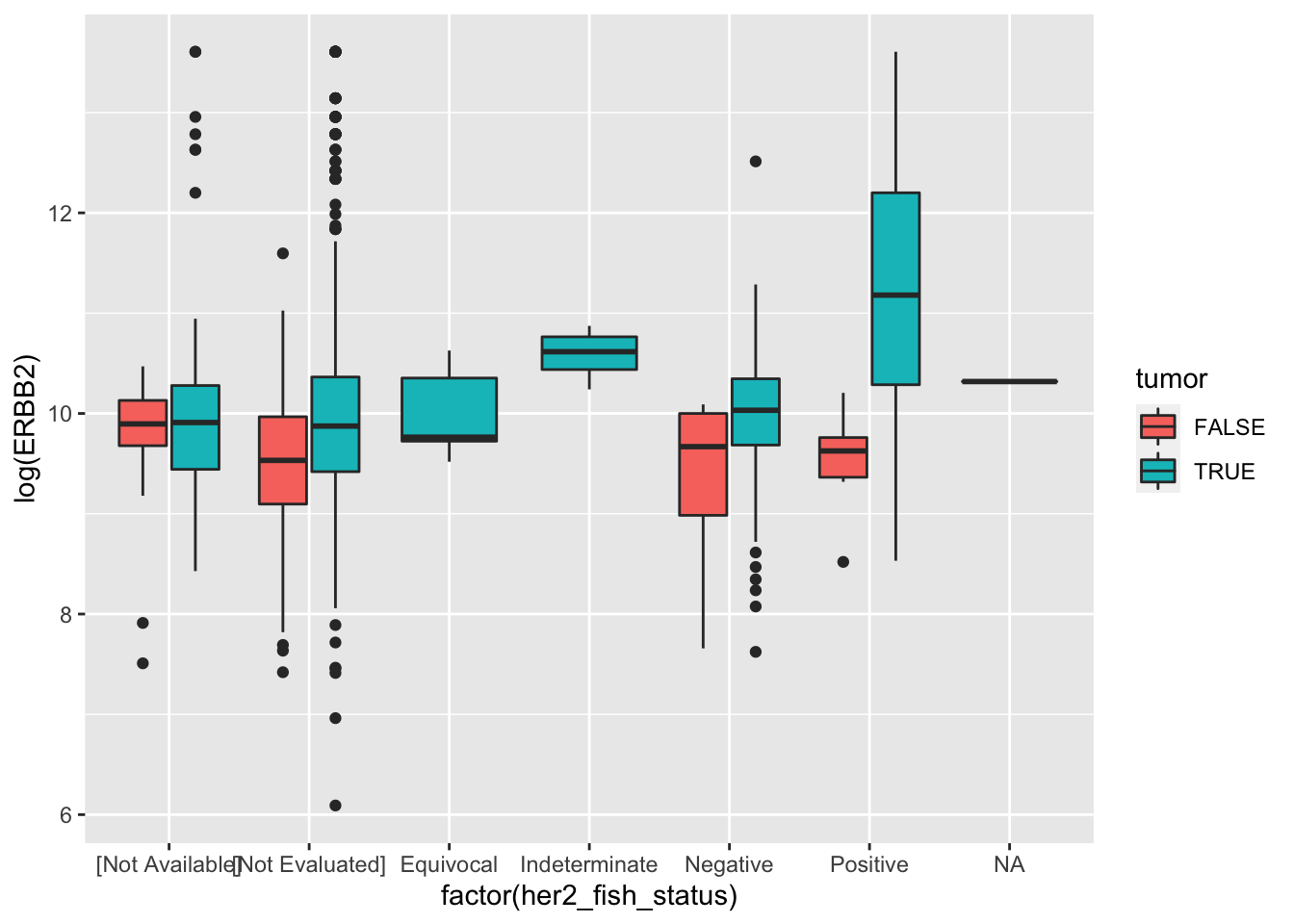

HER2 gene expression is definitely higher in tumors than in nomral tissue. Also HER2 fish status largely agrees with the gene expression data.

Question 9 [5 points]

The expression of \({\tt GRB7}\) and \({\tt ERBB2}\) are highly correlated. We will revisit the concept of correlation later in the course, but for now you can see a (positive) linear relationship between the two. Using \({\tt PubMed}\) or other resources, can you hypothesize why these two genes have such high correlation in their expression (what is the biological reason that their expression is correlated)?

Answer Since both genes are located on chromosome 17q in a close distance to each other, any amplification of that region would result in co-amplification of both genes together. Therefore, there is a high correlation in their expression. This region is part of the so-called HER2-amplicon and is frequently amplified in breast cancer (\(\tilde 15\%\)).

Question 10 [10 point] Suppose there are three friends who are discussing the possibilty of going on vacation together. We can call these individuals \(X, Y, Z\). Each friend has two issues to resolve: money, time. These are both logical variables themselves. For example, the money issue for \(X\) can be a logical variable \(XM\) and it is \({\tt TRUE}\) if and only if \(X\) has enough money. Similarly, the time issue is a logical variable \(XT\) that is \({\tt TRUE}\) if and only if \(X\) has enough vacation time.

So you might have R code that looks like this.

XM <- TRUE; XT <- FALSE; YM <- TRUE; YT <- TRUE; ZM <- FALSE; ZT <- FALSE

In this particular assignment of \({\tt TRUE}\) and \({\tt FALSE}\) to the variables, it is the case that only \(Z\) does not have enough money. There are many other asignments that are possible. For instance, it might be the case as follows

XM <- TRUE; XT <- TRUE; YM <- TRUE; YT <- TRUE; ZM <- TRUE; ZT <- TRUE

I would like you to write a logical expression in R code that evaluates to \({\tt TRUE}\) (they will go on vacation) or \({\tt FALSE}\) (they will not go on vacation) for each of the condition below.

  1. The condition is that all three people have enough money and enough time.

XM<-T; XT<- T; YM<-T; YT<- F; ZM<- F; ZT<-T
((XM&XT)&(YM&YT)&(ZM&ZT))
## [1] FALSE
  1. The condition is that all three people have enough money but time does not matter. (Maybe they decide to go for a weekend instead of two weeks.)
((XM&YM)&ZM)
## [1] FALSE
  1. The condition is that all three people have enough time but at least one person must have enough money. (The rich one will pay for the other two.)
(((XT&YT)&ZT) & ((XM|YM)|ZM))
## [1] FALSE
  1. The condition is that all three people have enough time but at least two people must have enough money.
(((XT&YT)&ZT) & ((XM&YM)|(XM&ZM)|(YM&ZM) ) )
## [1] FALSE

Good luck!